ALGORITMOS DE PLANIFICACION

Primero llegado, primero servido (FCFS)

Este algoritmo da servicio a las solicitudes de acceso a disco de la cola según el orden de llegada. Esta planificación hará uso de una cola tipo FIFO (First In, First Out – Primero en entrar, primero en salir).

Cuando se tiene que elegir a qué proceso asignar la CPU se escoge al que llevara más tiempo listo. El proceso se mantiene en la CPU hasta que se bloquea voluntariamente.

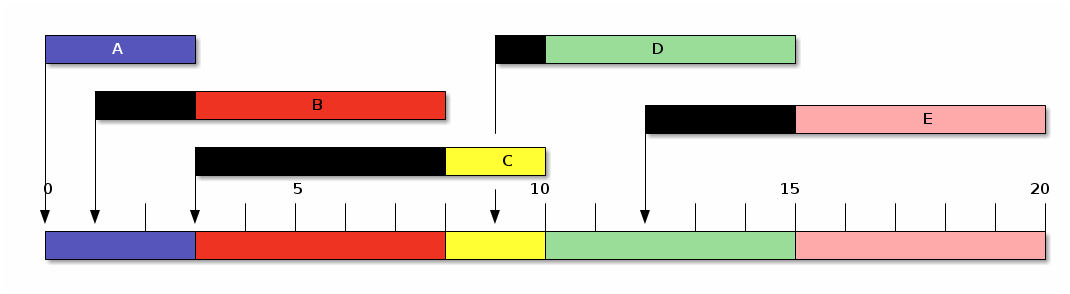
La ventaja de este algoritmo es su fácil implementación, sin embargo, no es válido para entornos interactivos ya que un proceso de mucho cálculo de CPU hace aumentar el tiempo de espera de los demás procesos . Para implementar el algoritmo (ver figura 2) sólo se necesita mantener una cola con los procesos listos ordenada por tiempo de llegada. Cuando un proceso pasa de bloqueado a listo se sitúa el último de la cola.

En a) el proceso P7 ocupa la CPU, los procesos P2, P4 y P8 se mantienen en la lista de preparados. En b) P7 se bloquea (ya sea al realizar una E/S, una operación WAIT sobre un semáforo a cero u otra causa) y P2 pasa a ocupar la CPU. En c) ocurre un evento (finalización de la operación de E/S, operación SIGNAL, ...) que desbloquea a P7, esto lo vuelve listo, pasando al final de la cola de procesos listos.

El esquema más simple de planificación es el Primero llegado, primero servido (First come, first serve, FCFS). Este es un mecanismo cooperativo, con la mínima lógica posible: Cada proceso se ejecuta en el órden en que fue llegando, y hasta que suelta el control. El despachador es muy simple, básicamente una cola FIFO. 

 

Round Robin

Round-robin es un método para seleccionar todos los elementos en un grupo de manera equitativa y en un orden racional, normalmente comenzando por el primer elemento de la lista hasta llegar al último y empezando de nuevo desde el primer elemento. El nombre del algoritmo viene del principio de Round-Robin conocido de otros campos, donde cada persona toma una parte de un algo compartido en cantidades parejas.
Una forma sencilla de entender el Round-robin es imaginar una secuencia para "tomar turnos". En operaciones computacionales, un método para ejecutar diferentes procesos de manera concurrente, para la utilización equitativa de los recursos del equipo, es limitando cada proceso a un pequeño período (quantum), y luego suspendiendo este proceso para dar oportunidad a otro proceso y así sucesivamente. A esto se le denomina comúnmente como Planificación Round-Robin.


El esquema round Robin busca dar una relación de respuesta buena tanto para procesos largos como para los cortos. La principal diferencia entre la ronda y FCFS es que en este caso sí emplearemos multitarea preventiva: A cada proceso que esté en la lista de procesos listos lo atenderemos por un sólo quantum (q). Si un proceso no ha terminado de ejecutar al final de su quantum, será interrumpido y puesto al final de la lista de procesos listos, para que espere a su turno nuevamente. Los procesos que nos entreguen los planificadores a mediano o largo plazo se agregarán también al final de esta lista.

Con la misma tabla de procesos que encontramos en el caso anterior (y, por ahora, ignorando la sobrecarga administrativa provocada por los cambios de contexto), obtendríamos los siguientes resultados: 

 

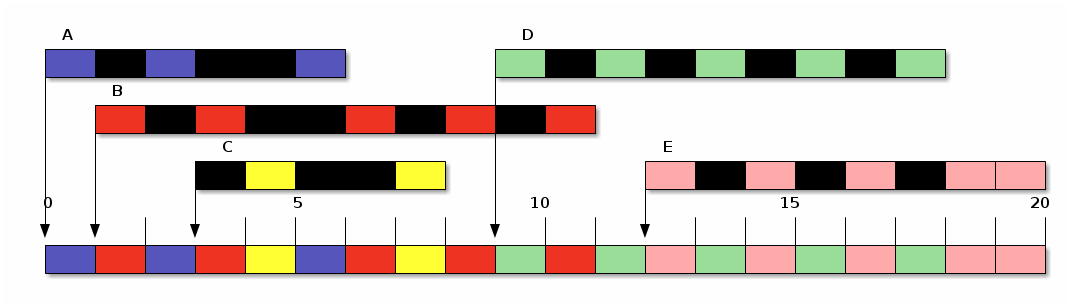
El round Robin puede ser ajustada modificando la duración de q. Conforme incrementamos q, la ronda tiende a convertirse en FCFS — Si cada quantum es arbitrariamente grande, todo proceso terminará su ejecución dentro de su quantum; por otro lado, conforme decrece q, mayor frecuencia de cambios de contexto tendremos; esto llevaría a una mayor ilusión de tener un procesador dedicado por parte de cada uno de los procesos, dado que cada proceso sería incapaz de notar las ráfagas de atención que éste le da (avance rápido durante un periodo corto seguido de un periodo sin avance). Claro está, el procesador simulado sería cada vez más lento, dada la fuerte penalización que iría agregando la sobrecarga administrativa. 

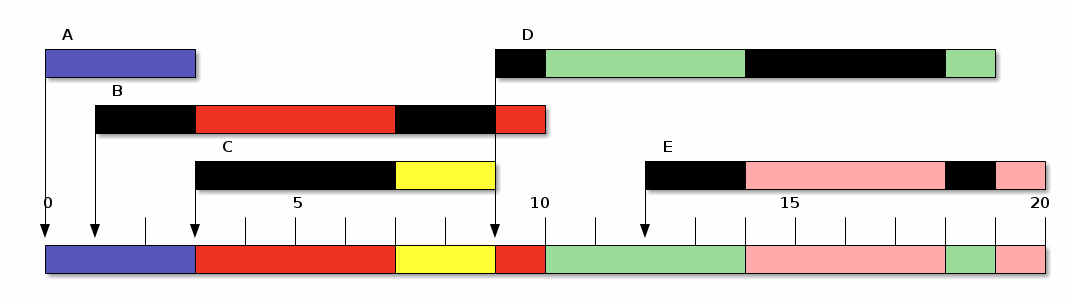
Si repetimos el análisis anterior bajo este mismo mecanismo, pero con un quantum de 4, obtendremos: 

 

El proceso más corto (SPN) Shortest Process Next

Esta es la versión no apropiativa del SPN, en la que el planificador siempre elige al proceso que le queda menos tiempo esperado de ejecución. Por lo tanto, el planificador debe disponer de una estimación del tiempo de proceso para poder llevar a cabo la función de selección, existiendo el riesgo de inanición para procesos largos.

El algoritmo SRT no presenta el sesgo favorable a los procesos largos del FCFS. Al contrario que el turno rotatorio, este algoritmo es más eficiente debido a que no se produce overhead muy frecuente debido a que las interrupciones no son producidos por el reloj del sistema. Por el contrario, se deben tener en cuenta los tiempos de servicio transcurridos, lo que contribuye a la sobrecarga. El SRT también debería producir tiempos de retorno mejores que los del SPN, puesto que los trabajos cortos reciben una atención inmediata y preferente a los trabajos largos.